流体
研究:
欧拉法
建模——理想流体无粘性、不可压缩
流速场——流动空间
流线——流线不可相交
流管——一个截面与流线形成的管状区域,流管是研究流体问题时重要的研究对象,可作为整体研究
连续性方程
伯努利方程
粘性流体
牛顿粘性定律:F=ηS·(dv/dz)
雷诺数:Re=ρvr/η
Re>2000湍流,Re<1000层流
斯克托斯定律:Ff=6πηrv
泊肃叶定律
Q=(πR^4/8ηL)(p1-p2) p1-p2系数的倒数是流阻
振动和波
简谐振动
振动方程:x=Acos(ωx+φ)
特征量:
ω=(k/m)^(1/2)=(g/l)^(1/2)(单摆)
相位 ωt+φ——初相
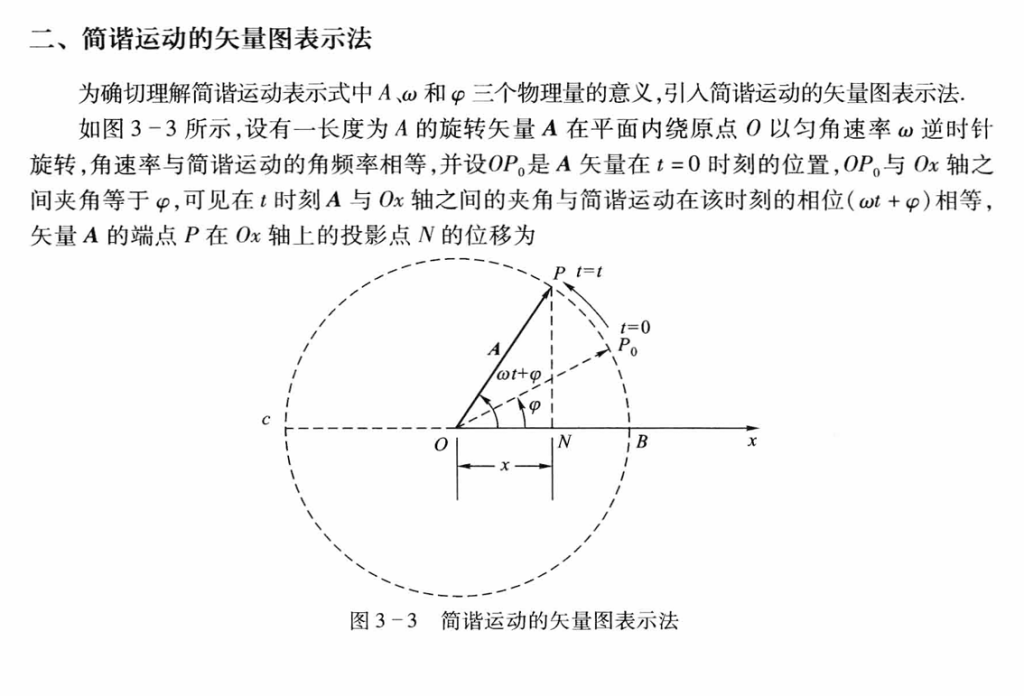
矢量图
简谐振动能量
E=Ek+Ep=(1/2)kA^2 k=mω^2
振动合成与分解
同方向同频率
x=x1+x2
两种特殊情况
同相,反相,振幅叠加
同方向不同频
振幅周期变化,变化的频率成为拍,拍频:v=v2-v1
波
波源、波线、波面,波面垂直于波线
波动方程:沿x轴正向传播:y=Acos[ω(t-x/v)+φ]=Acos[2π(t/T-x/λ)+φ]
沿x轴逆向传播:y=Acos[ω(t+x/v)+φ]=Acos[2π(t/T+x/λ)+φ]
同一质点在两个相邻时刻相位差:Δφ=(Δt/T)·2π
波的能量
波的能量密度:w=ρA^2ω^2sin^2ω(t-x/u) 平均能量密度需要将sin转化为有效值,再平方
波强:I=w平均·u=(1/2)ρA^2ω^2u 单位:w/m^2
波的衰减
反平方定律:I1/I2=r2^2/r1^2波强和半径的平方成反比
波的干涉
两同频同向同相波才是相干波源
Δφ=2kπ,增强,Δφ=(2k+1)π,减弱
声波
声压:幅值:p=ρuAω,有效值:除根号2
声阻:Z=ρu
声强:I,定义为一个波动周期内单位时间通过垂直于声波传播方向上的单位面积的声波能量,与波强同表达式,也可表示为Pe^2/Z(Pe为声压有效值,Z为声阻
反射系数与透射系数:
声强级和响度级
L=lg(I/I0) 单位:贝尔 B
L=10lg(I/I0) 单位:分贝 dB
I0=10^-12 W/m^2
多普勒效应
去看书,大概率不考 两个公式:L=a^2/λ sinθ=0.61λ/a(a为探头半径,L为近场长度
光的波动性
杨氏双缝干涉实验
光程
折射率的另一种表示:n=λ/λ’
光程(s)
s=nL=(λ/λ’)L
光程差
Δs=n2r2-n1r1
相位差
Δφ=(2π/λ)Δs
此处λ为真空中光的波长
对干涉现象的补充:将波程差换为光程差,波长为真空波长。光程差为半波长的偶数倍是光强极大点,奇数倍是光强极小点
薄膜干涉
分等倾和等厚,等倾干涉的干涉结果只与入射角有关,等厚干涉的干涉结果只与厚度有关
垂直入射时,Δs=2dn+λ/2
n为穿过再反射的介质折射率,需注意,两次反射是否都是光疏到光密,若是,公式中没有最后一项,若不是,有最后一项